Find x in the following figures.

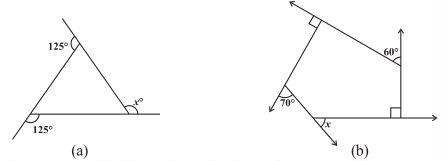
(a) 

125° + m = 180° ⇒ m = 180° – 125° = 55°   (Linear pair)

125° + n = 180° ⇒ n = 180° – 125° = 55°   (Linear pair)

x = m + n   (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)

⇒ x = 55° + 55° = 110°

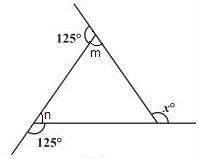
(b) 

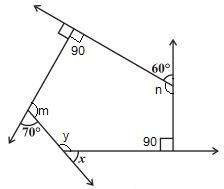
Two interior angles are right angles = 90°

70° + m = 180° ⇒ m = 180° – 70° = 110°   (Linear pair)

60° + n = 180° ⇒ n = 180° – 60° = 120°   (Linear pair) 

The figure is having five sides and is a pentagon.

Sum of the angles of a pentagon = 540°

⇒ 90° + 90° + 110° + 120° + y = 540°

⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°

x + y = 180°   (Linear pair)

⇒ x + 130° = 180°

⇒ x = 180° – 130° = 50°

(a) 

125° + m = 180° ⇒ m = 180° – 125° = 55°   (Linear pair / रैखिक जोड़ी)

125° + n = 180° ⇒ n = 180° – 125° = 55°   (Linear pair / रैखिक जोड़ी)

x = m + n   (त्रिभुज के बाहरी कोण का मान विपरीत आंतरिक कोणों के योग के बराबर होता है)

⇒ x = 55° + 55° = 110°

(b)

दो आंतरिक कोण समकोण हैं = 90°

70° + m = 180° ⇒ m = 180° – 70° = 110°   (Linear pair / रैखिक जोड़ी)

60° + n = 180° ⇒ n = 180° – 60° = 120°   (Linear pair / रैखिक जोड़ी)

आकृति पाँच भुजाओं वाली है और एक पंचभुज (pentagon) है।

पंचभुज के कोणों का योग = 540°

⇒ 90° + 90° + 110° + 120° + y = 540°

⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°

x + y = 180°   (Linear pair / रैखिक जोड़ी)

⇒ x + 130° = 180°

⇒ x = 180° – 130° = 50°