What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
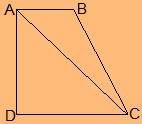
Let $ABCD$ be a convex quadrilateral.
From the figure, the quadrilateral $ABCD$ can be split into two triangles:
i.e. $\triangle ADC$ and $\triangle ABC$.
Since the sum of interior angles of a triangle = $180^\circ$,
Sum of angles of $ABCD$ = $180^\circ + 180^\circ = 360^\circ$.
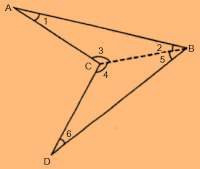
Now take a non-convex (concave) quadrilateral $ABCD$. Join $BC$ so that it divides $ABCD$ into two triangles $\triangle ABC$ and $\triangle BCD$.
In $\triangle ABC$,
$\angle 1 + \angle 2 + \angle 3 = 180^\circ$.
In $\triangle BCD$,
$\angle 4 + \angle 5 + \angle 6 = 180^\circ$.
Therefore,
$\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 + \angle 6 = 180^\circ + 180^\circ$
$\Rightarrow$ $\angle A + \angle B + \angle C + \angle D = 360^\circ$.
Hence, the sum of interior angles of any quadrilateral (convex or non-convex) is $360^\circ$.
एक उत्तल (convex) चतुर्भुज के कोणों के माप का योग क्या है? क्या यह गुण नहीं-उत्तल (non-convex/concave) चतुर्भुज के लिए भी रहेगा? (एक non-convex चतुर्भुज बनाकर आजमाइए!)

मान लीजिए $ABCD$ एक उत्तल चतुर्भुज है।
चित्र से स्पष्ट है कि चतुर्भुज $ABCD$ को दो त्रिभुजों में बाँटा जा सकता है:
यानी $\triangle ADC$ और $\triangle ABC$।
त्रिभुज के अन्तः कोणों का योग = $180^\circ$ है।
अतः $ABCD$ के कोणों का योग = $180^\circ + 180^\circ = 360^\circ$।

अब एक गैर-उत्तल (concave) चतुर्भुज $ABCD$ लें और $BC$ को जोड़ें ताकि यह $ABCD$ को $\triangle ABC$ और $\triangle BCD$ में बाँट दे।
$\triangle ABC$ में,
$\angle 1 + \angle 2 + \angle 3 = 180^\circ$।
$\triangle BCD$ में,
$\angle 4 + \angle 5 + \angle 6 = 180^\circ$।
अतः,
$\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 + \angle 6 = 180^\circ + 180^\circ$
$\Rightarrow$ $\angle A + \angle B + \angle C + \angle D = 360^\circ$।
निष्कर्ष: किसी भी चतुर्भुज (उत्तल या गैर-उत्तल) में अन्तः कोणों का योग $360^\circ$ होता है।
